Do Sweat The Small Stuff!

Uncategorized 4 Minutes

Three years after visiting Shanghai, what has stuck with me? (Part 2)

In 2015, my colleague (@Carohami) and I took part in an England-China teacher exchange programme, organised by the Maths Hubs.  In this series of posts, I reflect on some of the things that have stuck with me over the last three years.

***

In some ways, planning a mathematics lesson is a bit like staring at a fractal.

Fractal Triangle 2The mathematics curriculum is often separated into large sections, such as Number, Data, Algebra etc.  Each section tends to be split into subsections that might be referred to as topics, chapters or units of work: introduction to fractions, equivalence, four operations with fractions, and so on.  Within each unit students learn a set of skills, concepts and procedures, such as how to add fractions, how to multiply them, etc.  When teachers plan to teach each of these skills, we often break them down into a series of small steps (e.g. learning to add fractions might be broken down into adding like fractions, then related fractions, then unrelated fractions, mixed numbers and so on).  And then within each small step there are lots of even finer points.  When adding related fractions, how do you decide which fraction to change? Once you’ve added the fractions, how do you spot if the total is a whole number?

This fractal analogy is far from perfect! But it aims to emphasise those tiny parts of mathematics that can be hard to spot unless you deliberately focus on them.  It was these fine details that I reckon overlooked on too many occasions at the start of my teaching career.  I probably still miss a fair few now.

Sometimes I would presume that students would just pick up the fine details along the way, while learning bigger things.  For example, I presumed that students would just pick up what it means for two algebraic terms to be ‘like’ while they are busy ‘collecting like terms’.  

Collecting Like TermsOr they would learn how identify which angles in isosceles triangles are equal while solving missing angle problems.  

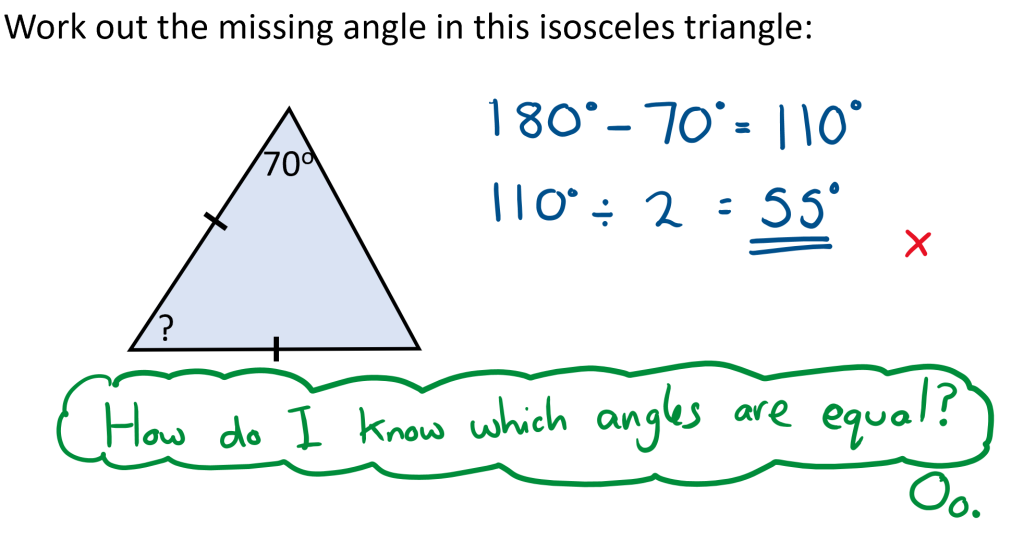
Isoscelese Triangle

Even when I did cover these points, on reflection, I don’t think I gave them as much time as they needed.

Other times, fine details would crop up sporadically and cause problems while students were working through an exercise.  For example, when students were practising to rearrange formulae and a question such as the one below came up, students assumed that they had made a mistake because their answer didn’t match the textbook’s answer. 

Formula

When I tried to reassure them that they were right, some would then ask, “So are there two correct answers then?”  I would then frantically try to convince them that both fractions were identical.

There were even small details that I was completely oblivious to.  Throughout my own GCSEs, A-levels, university degree and first few years of teaching, I thought that alternate angles and corresponding angles only existed between parallel lines. Reassuringly, I wasn’t alone with this!  It was only when I read an article by Huang and Leung (link at the bottom) that I learned that the lines don’t have to be parallel for the angles to be corresponding; parallel lines is just the special case when corresponding angles are equal.

Corresponding Angles

One thing struck me about the lessons I saw in Shanghai was how they paid special attention to little things.  On numerous occasions, the teacher would dedicate part of a lesson to discussing a tiny, tiny aspect of a topic and then get the students to practise that point in isolation before applying it to bigger questions.  These moments would only take up a few minutes of the lesson, but they were enough to prepare students for the more complex problems ahead. They taught each detail explicitly!

Here are some examples from the lessons we visited:

1. By spending enough time on these points:

(m-n) = –(n-m)     and      –(m-n) = (n-m)

students were better prepared to deal with situations like this:
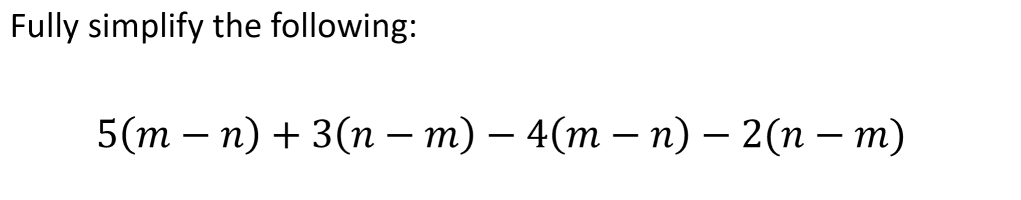
Simplify brackets

2. In a lesson on multiplying terms with indices, the teacher started by asking the following:
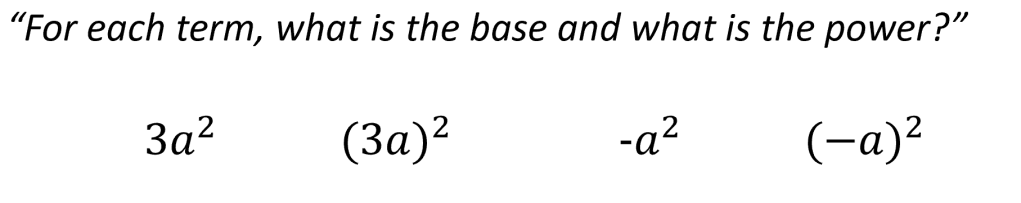
Base and Power

3. There was an exercise that solely practised applying powers to negatives:
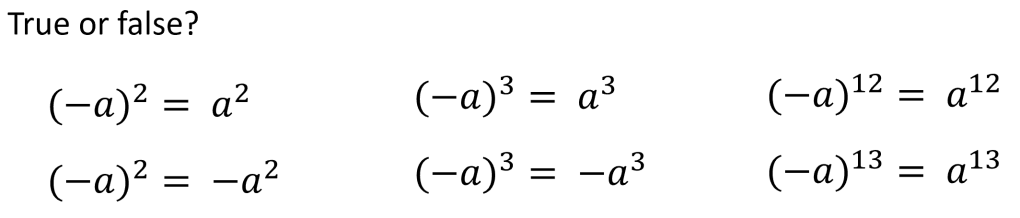
True of false

4. By tackling points 2 and 3 in advance,  students were equipped to tackle these questions:
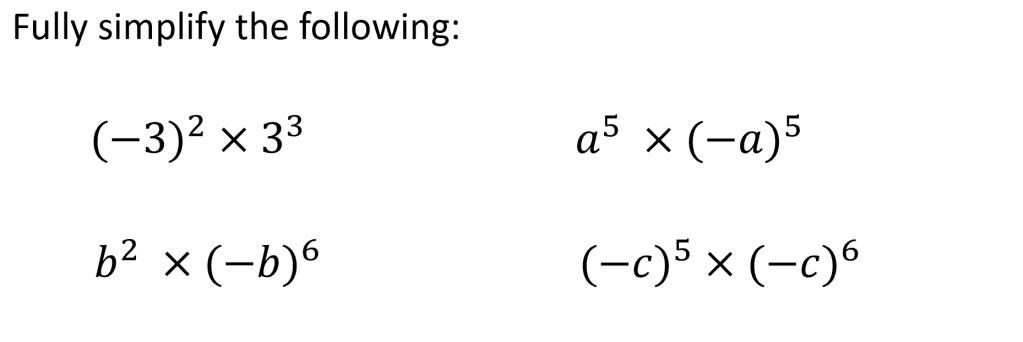
Indices

5. Once students were confident on all of the previous points, this next question became straight forward:

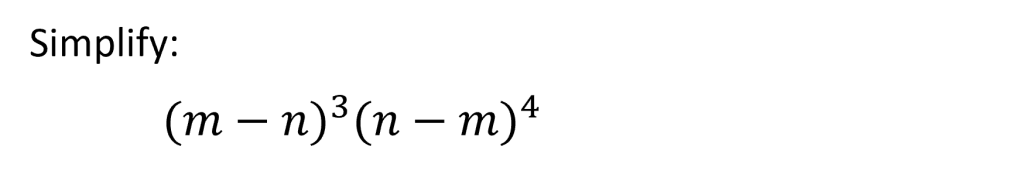
Bracket Indices 2

There are so many tiny points like these in mathematics that addressing each of them separately would completely atomize the curriculum.  I’m not yet sure about how wise that would be.  Is it necessary for every single student to cover every single tiny point explicitly like this? Probably not. I’m not sure it’s even possible in the available time.  Then again, I find that students’ misconceptions are often caused by misunderstanding one of these tiny aspects of the topic.

If there’s one thing I’m certain about, it’s that the trip to Shanghai highlighted the importance of the little things.  On reflection, the reason why I probably didn’t think so much about these little things was because, as an experience mathematician, I didn’t need to think about them – the more experienced we get with something, the more we automate and the less we need to think about what we’re doing.  But my students are not expert mathematicians; they’re learning.  So the Shanghai exchange has encouraged me to pay more attention to the fine details and think carefully about if, when and how I should address them.

If you found this post interesting, then I would also recommend the following:

Previous blog posts:

This series, ‘What I Learned From Shanghai’:

‘Making Connections’ Series:

‘Planning Topics’ Series:

Published by Pondering Planning

Published